Pole-Zero placement

Use the new, improved pole-zero calculator—but be sure to read the “Experiments with standard biquads” section below for tips on placing poles and zeros for standard filters.

Here’s a Java applet that illustrates pole-zero placement. It lets you design a filter with two poles and two zeros, while showing the resulting frequency response and filter coefficients. It’s also handy for learning more about how poles and zeros work.

You can set the two poles (or zeros) independently, or as complex conjugate pairs by using the Pair checkboxes. Note that the frequency response plot and the coefficients are gain compensated automatically, so that the maximum output is 0 dB.

A pole or zero located at the origin has no effect, so position them there if you want to disable them (to examine single pole or zero filters, for instance).

Experiments with standard biquads

Here are some experiments that show how the standard biquads (derived with the bilinear transform) relate to the z plane.

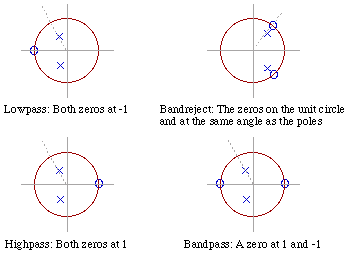
For each of these filters, the pole angle dictates filter frequency, and the pole radius dictates Q:

Experiment with pole and zero placement to better understand how these filters work. See what happens when you swap the poles and zeros. Change the pole angle and radius and see how it affects the frequency response. Think about why the poles and zeros are positioned where they are: For lowpass, the zeros are at -1 to pull down the response at the highest frequency; for highpass, they are at 1 to pull down the lowest; for bandpass, they pull down the response at each end of the spectrum. For bandreject (notch), the zeros are on the unit circle at the notch frequency to completely remove it, and the poles are at the same angle; as the poles move closer to the zeros, they get closer to canceling them, and the notch narrows.