There’s another issue with floating point hardware that can easily cause serious performance problems in DSP code. Fortunately, it’s also easy to guard against if you understand the issue. I covered this topic a few years ago in A note about de-normalization, but giving it a fresh visit as a companion to Floating point caveats.
Floating point hardware is optimized for maximum use of the mantissa, for best accuracy. (It also allows for more efficient math processing, since the mantissas are always aligned.) This is called normalization—all numbers are kept in the binary range of plus or minus 1.1111111 (keep going, 16 more 1s) times 2 raised to the power of the exponent. To increase accuracy near zero, floating point implementations let the number become “denormalized”, so instead of the smallest number being 1.0 times 2 raised to the most negative exponent, the mantissa can become as small as 0.000…1 (24 digits).
The penalty is that floating point math operations become considerably slower. The penalty depends on the processor, but certainly CPU use can grow significantly—in older processors, a modest DSP algorithm using denormals could completely lock up a computer.
But these extremely tiny values are of no use in audio, so we can avoid using them, right? Not so easily—recursive algorithms such as IIR lowpass filters can decay into near-zero numbers in typical use, so they will happen. For instance, when you hit Stop on your DAW’s transport, it likely sends a stream of zeros (to let reverbs decay out, and any live input through effects to continue). The memory of a lowpass filter then decays exponentially towards zero. We can slow it a bit by using double precision floats, but it’s only a matter of time till the processing meter climbs abruptly when your processing algorithm bogs down in denormalized computation.
Modern processors can mitigate the problem with flush-to-zero and denormals-are-zero modes. But this too can be tricky—you’re sharing the processor with other functions that might fail without the expected denormal behavior. You could flip the switch off and back during your main DSP routine, but you need to be careful that you’re not calling a math function that might fail. Also, this fix is processor dependent, and might be the wrong thing to do if you move your code ot a new platform. A DSP framework might handle this conveniently for you, but my goal here is to show you that it’s pretty easy to work around, even without help from the processor. Let’s look at what else we could do.
We could test the output of any susceptible math operation—there is no need to test all operations, because most won’t create a denormal without a denormal as input.
There’s a surprisingly easy solution, though, and it’s more efficient than testing and handling each susceptible operation. At points that have the threat of falling into denormals, we can add a tiny value to ensure it can’t get near zero. This value can be so small that it’s hundreds of dB down from the audio level, but it’s still large compared with a denormal.
In fact, it’s actually possible to flush denormals to zero with no other error, due to the same properties of floating point we discussed earlier. If you add a relatively large number to a denormal, then subtract it back out, the result is zero. Still, this is pointless, because a tiny offset will not be heard.
But there is a catch to watch out for. A constant value in the signal path is the same as a DC offset. Some components, such as a highpass filter, remove DC offsets. I get around this by using a tiny number to add as need in the signal path—often, one time is enough for an entire plugin channel—and alternating the sign of it each time a new buffer is processed. A value such as 1e-15 (-300 dB) completely wipes out denormals while having no audible effect.
Why did I pick that value? It needs to be at least the smallest normalized number (2^-126, about 1e-38, or about -760 dB), to ensure it wipes out the smallest denormal. That would work, but it’s better to use a larger number so that you don’t have to add it in as often. A much larger number would likely be fine to add just once—just add it to the input sample, for instance. (But consider your algorithm—if you have a noise gate internal to your effect, you might need to add the the “fixer” value after its output as well.) And clearly it needs to be small enough that it won’t be heard, and won’t affect algorithms such as spectrum analysis. A number like 1e-15 is -300 dB—each additional decimal place is -20 dB, so 1e-20 is -400 dB, for instance. Let your own degree of paranoia dictate the value, but numbers in those ranges are unlikely to affect DSP algorithms, while wiping out any chance of denormals through the chain.
To recap: Take a small number (mDenormGuard = 1e-15;). Change its sign (mDenormGuard = -mDenormGuard;) once in a while so a DC blocker you might have in your code doesn’t remove it. A handy place is the beginning of your audio buffer handling routine, one sign change for an entire buffer should be fine. Add it in (input + mDenormGuard).
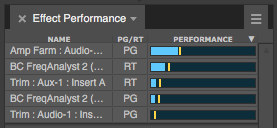
Here’s an example of my plug-in (Amp Farm native), during development, showing the performance meter in a DAW while processing audio:
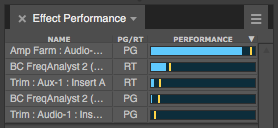
With denormal protection turned off, the performance is the same while processing normal audio, but a few seconds after stopping the transport, the load rises due to denormals:
With denormal protection enabled, performance looks like the first picture at all times. And that’s why we protect against denormals!


Great having this introduction to denormals, i also read that ieee floats support (but i reckon not mandate) this. You talk about the possibility of flipping the switch off and back. Is this some hardware register? What kind of algorithms actually would benifit from using denormals (as opposed to flushing to all zeroes?)
Yes, flush-to-zero and denormals-are-zero (whose idea were denormals anyway? Maybe a good thing for single precision, but once you have doubles, little practical use…life would be easier if the default was for denormals to be disabled). There’s plenty on the web on the topic. Not too much to go wrong if you just switch it in you audio processing routine, since you probably would be already avoiding calls to math library routines that might care.
Maybe my question will sound a bit stupid, but why are denormals causing a slowdown? I understand what denormal float number is, but I do not see the point where the performance decrease comes from? All float instructions should take still the same amount of time to execute, whether normalized or not. (Mind you please, I come from the embedded MCU world, not sure much how our grand-dads x86 are doing).
Thank you for a hint,
Jan
Denormals are usually not handled in hardware, but as an exception, executing in microcode.
Hope it’s OK if I shamelessly plug my Undenormal project? I read so many interesting and helpful things on your blog over the years, thank you so much by the way, maybe someone can gain or learn something from this in return. 🙂
https://github.com/rcliftonharvey/rchundenormal
It’s a primitive class that does just what you mention in your text, it “flips the switch on and off” for FTZ and DAZ. Instantiate the class in a block of code, and it sets the CPU registers to disable denormal numbers. As soon as the class instance goes out of scope, or its destructor is called, the CPU registers are set to enable denormal numbers again.
Note that disabling denormal numbers breaks IEEE standard compliance, so it’s a good thing to keep them enabled until they really shouldn’t be, and to also enable them again when they no longer pose a danger.
The FTZ and DAZ flags are part of the SSE2 instruction set, so they should not cause any issues on CPUs supporting SSE2, which today is essentially any CPU. I think Athlon XP and Pentium III might be problematic, anything after that should be fine. I have no clue about the situation ARM machines, never had an interest in those, but anything x86 compatible that’s in productive use today should be fine.
Although it’s obviously centered on gaming machines, which tend to be a bit more up-to-date than audio workstations, the Steam hardware surveys are always worth keeping an eye on when it comes to supported processor instruction sets.
https://store.steampowered.com/hwsurvey/Steam-Hardware-Software-Survey-Welcome-to-Steam
(Click the “other” entry at the bottom)
Thanks Rob!
Very interesting !
How often should the sign be flipped?
Each samples might be a bit overkill while after each buffer/block process it might take too long with longer buffers?
Typically just once per buffet. For instance, your DSP routine will get called with a buffer—just flip the tiny value at the start of the routine, then add the value to the input. We’re guarding against DC blockers, remember, by toggling the sign, and they are necessarily not fast acting (their job is to block the slowest changes, not fast ones). But if you know the processor you’ll be running on has the ability to flush denormals, that simplifies things.
| A handy place is the beginning of your audio buffer handling routine, one sign change for an entire buffer should be fine. Add it in (input + mDenormGuard).
Does this mean “Sample wise addition” or “once per buffer to one sample”?
i.e. I have a buffer:
0, 1, 0, -1
Does that buffer become
0 + 1e15, 1 + 1e15, 0 + 1e15, -1 + 1e15
And the next:
0 – 1e15, 1 – 1e15, 0 – 1e15, -1 – 1e15
Or:
0+ 1e15, 1, 0, -1
0 – 1e15, 1, 0, -1
Thanks for the great article!
Yes, the first one. Basically as I read out each sample from the input (like in a for looping, processing samples one at a time), I add the value. So every input sample gets the offset.